Задача A.
Вася винайшов просте шифрування тексту щоб мати можливість таємно та безпечно переписуватися з Тетяною. Ідея шифру полягає в зміні порядку голосних літер в тексті на протилежний. Формально після шифрування повідомлення “I love you” Тетяна отримає “U lovy eoi”, тобто остання голосна літера в тексті переміститься на позицію першої літери, а перша літера переміститься на позицію останньої літери.
Зверніть увагу на те, що регістр має відповідати регістру тої букви яку замінили. Повідомлення Василя може містити як великі так і малі літери латинського алфавіту, цифри та пробіли. Іноді до Васі приходить натхнення і він здатен написати повідомлення довжини 2 * 107 символів.
Ваша задача написати програму, яка буде слугувати Василеві шифратором, а Тетяні - дешифратором, для здійснення безпечного листування.
Літери {A, E, I, O, U, Y} будемо вважати голосними.
Вхідні дані:
В першій стрічці записане число N - довжина повідомлення ( 0 < N < 2 * 107).
В наступній стрічці записане саме повідомлення, яке містить великі та малі літери алфавіту, цифри та пропуски.
Вихідні дані:
Стрічка зі зміненим порядком голосних літер латинського алфавіту.
Приклади
| Приклад 1 | Приклад 2 |
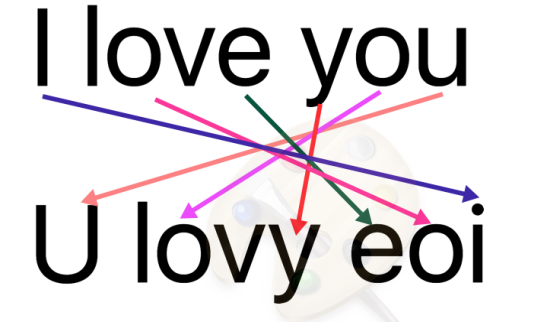 |
 |
Задача B.
На столі лежать магічні кристали з різними енергетичними зарядами. Пронумеруємо кристали від 0 до N. Тоді e[0], e[1], e[2], … e[N] - послідовність зарядів магічних кристалів.
Магічні кристали не можна переміщати, а можна лише обєднувати з сусідніми кристалами. Коли ми об’єднуємо два сусідніх кристала або неперервну послідовність кристалів - на їх місці утворюється новий кристал. Заряд нового кристала рівний сумарному заряду кристалів які його утворили.
Василько лише новачок в темній магії, і знає лише одне закляття яке спроможний здійснити лише один раз.
Перед тим як вимовити закляття, Василько загадує проміжок [i, j].
Закляття виконує дві дії:
1) Об’єднує всі кристали на проміжку [i, j], тобто на їхньому місці утворюється новий кристал з зарядом E = e[i] + e[i + 1] + e[i + 2] + … + e[j].
2) Всі кристали, які поза цим проміжком, - зникають.
Василько зацікавився, а скільки існує різних способів застосувати закляття до кристалів на столі, щоб кожен такий спосіб давав в результаті - магічний кристал, заряд якого лежав би в межах [a, b].
(Формально скільки різних проміжків [i, j] можна загадати перед застосуванням закляття, щоб результуючий заряд кристала лежав в проміжку [a,b].)
Вхідні дані:
В першому рядку задається N - кількість кристалів. (0 < N < 2*106)
В другому рядку значення a та b. (-1018 < a, b < 1018)
В наступному рядку e[0], e[1], … , e[N - 1] - послідовність зарядів кристалів. ( |e[i]| < 109, i in [0, n - 1])
Вихідні дані:
Виведіть число - відповідь на задачу.
Приклади
| Вхідні дані | Вихідні дані |
| 3 -2 0 -1 3 -2 |
3 |
Пояснення до прикладу:
[i, j] = [0, 0] => -1 належить [-2, 0]
[i, j] = [0, 2] => -1 + 3 + (-2) = 0 належить [-2, 0]
[i, j] = [2, 2] => -2 належить [-2, 0]
Задача C.
Поліна займається геологією але досить часто їй зустрічаються задачі, які без допомоги програміста дуже важко вирішити. І цей раз не виключення.
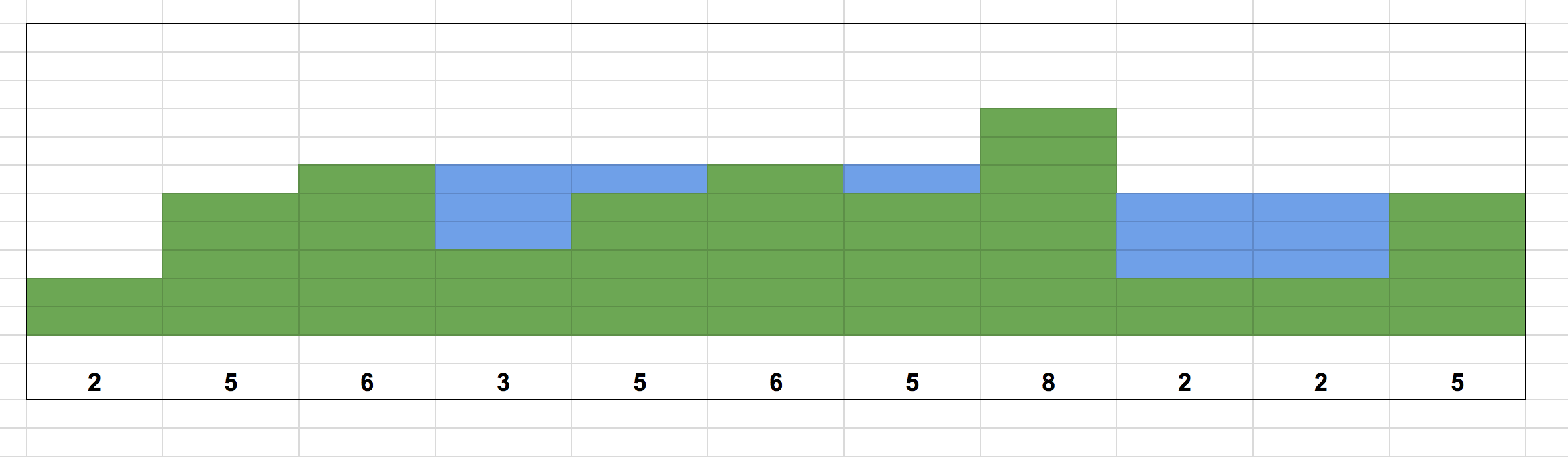
У Поліни є схема поверхні частини гірської місцевості. Дану частину гірської місцевості розбили на рівні інтервали, довжина кожного інтервалу становить 1 метр. Схема задається послідовністю чисел, де кожне число визначає висоту і-го інтервалу в метрах. Поліну попросили визначити об’єм води, який осяде, після тривалих опадів в цій гірській місцевості.
Вхідні дані:
Перший рядок містить чисто n - кількість інтервалів на схемі. (0 < n < 2 * 106)
Наступний рядок містить послідовність h[0], h[1], …, h[n - 1], де h[i] - висота і - того інтервалу. ( 0 <= h[i] < 109, i = 0..n - 1)
Вихідні дані:
Повинні містити одне число – об’єм води який осяде на гірській місцевості.
Приклади
| Вхідні дані | Вихідні дані |
| 11 2 5 6 3 5 6 5 8 2 2 5 |
11 |
Задача D.
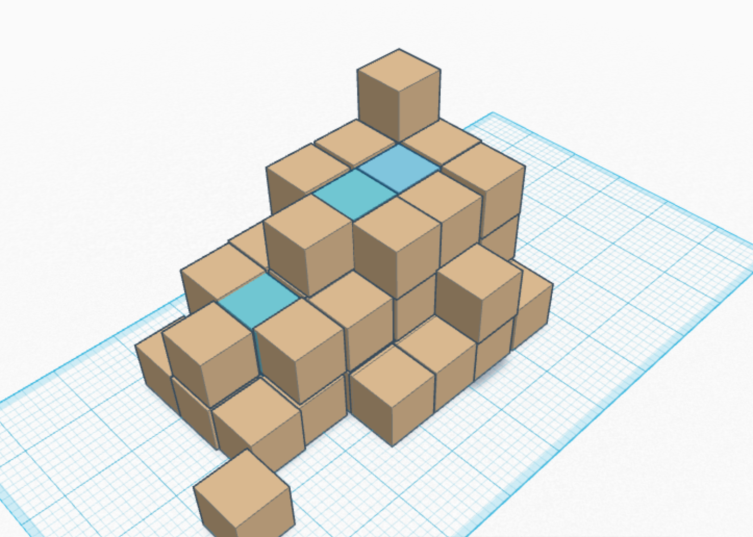
Петро дуже розумний програміст, який наважився допомогти геологам в вирішенні попередньої задачі. Сьогодні йому прийшло прохання допомогти в дуже схожій проблемі, а саме написати програму яка підраховує кількість води, яка осяде в гірській місцевості, але на цей раз, схема задається знімком зі супутника, і представляє собою матрицю, кожна клітинка якої визначає висоту (в метрах) ділянки землі - 1х1 метрів.
Вхідні дані:
Перший рядок містить два числа n, m - розміри матриці (0 < n, m < 1100).
Наступні n рядків містять по m чисел - висота кожної ділянки матриці.
Висота кожної ділянки землі - це число від 0 до 10000.
Наступні n рядків містять по m чисел - висота кожної ділянки матриці.
Вихідні дані:
Виведіть одне число - сумарний об’єм води яка осяде.
Гарантується, що результат - число від 0 до 2 * 109.
Приклади
| Вхідні дані | Вихідні дані |
| 3 6 1 4 3 1 3 2 3 2 1 3 2 4 2 3 3 2 3 1 |
4 |
Задача E. "Число 7"
Послідовність Фібоначчі починається так: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233… Магічним числом назвемо число, яке є числом Фібоначчі і кратне семи.
Вхідні дані:
Стандартний потік містить числа, що є номерами чисел Фібоначчі. Числа записані через пропуск.
Вихідні дані:
У стандартний потік записати 1 - якщо число Фібоначчі має своїм дільником число 7, та 0 - у противному випадку. Заносити у потік числа слід без пропусків.
Приклади
| Вхідні дані | Вихідні дані |
| 8 5 | 10 |
