Задача A. k-та цифра.

Степан написав програму, яка вирішує наступну задачу: за даними числами a, b, N вивести послідовність чисел a, a+b, a+2b, ..., a+Nb. Звісно, що Степан, як завжди, заклопотаний своїми проблемами, допустив помилку, а саме забув вивести пробіл для розділу між числами, в результаті чого отримався довгий рядок з цифр. Щоб не виправляти помилку, Степан вирішив з'ясувати, як знайти k-ту цифру в утвореному рядку (нумерація цифр починається з одиниці).
Степан не зміг знайти гарного рішення, тому просить допомоги у вас.

   Вхідні дані:
   У першому рядку знаходиться чотири цілих числа a, b, N, k (1 ≤ a, b ≤ 1000, 1 ≤ N, k ≤ 10⁹).

   Вихідні дані:
   Виведіть k-ту цифру рядка. Якщо довжина рядка менша за k, то виведіть -1.

   Приклади

Вхідні дані	Вихідні дані
3 5 6 9	2
2 7 2 10	-1

 

Задача В. Бонуси.

   Степан пристрасний любитель преферансу. У картковій грі «Преферанс» є цікава система бонусів, названа «за вірність грі». Суть її полягає в наступному: один раз на добу під час входу в гру гравець отримує бонус або в фішках (якими можна зробити ставку в грі), або золотими монетами (за які купуються додаткові послуги, наприклад, можливість змухлювати в грі «Підкидний дурень» ).
   Розмір бонусу обчислюється таким чином: рік ділиться на проміжки в 5 днів, i 1 січня вважається першим днем ​​проміжку. Для Степана, як елітного гравця, розмір бонусів нараховується таким чином:
   - в перший день - 1000 фішок;
   - у другий день - 5000 фішок;
   - в третій і четвертий день - по 3000 фішок;
   - в п'ятий день - 3 золоті монети.
   Степан вирішив підрахувати, скільки таких бонусів він отримав протягом року. На жаль, він заплутався і попросив учасників олімпіади допомогти йому.

   Вхідні дані:
   Перший рядок містить ознаку високосного року (1 - рік високосний, 0 - ні). У другому рядку записано число k - кількість днів, у які Степан грав у преферанс. Це число додатне і не перевищує кількості днів у відповідному році. Нарешті, наступні k рядків містять записи про дату гри в форматі «дд/мм». Ніякого сортування дат немає, як немає і повторюваних записів.

   Вихідні дані:
   Виведіть два числа: кількість фішок і золотих монет, зароблених Степаном за вірність грі.

   Приклади

Вхідні дані	Вихідні дані
1 5 01/01 31/03 10/02 31/12 06/08	7000 0
0 5 01/01 31/03 10/02 31/12 06/08	5000 6

 

Задача C. Дроби.

   Умову готував Степан, тому вона дуже проста.
   N дробів задані своїми чисельниками і знаменниками. Підрахуйте кількість різних дробів.

   Вхідні дані:
   Перший рядок містить число N (1 ≤ N ≤ 10⁵). Далі йдуть N рядків, у кожному з яких записано по два цілих числа A, B (-10⁹ ≤ A ≤ 10⁹, 1 ≤ B ≤ 10⁹) - чисельник і знаменник дробу.

   Вихідні дані:
   Виведіть одне число - кількість різних дробів.

   Приклади

Вхідні дані	Вихідні дані
6 3 9 -2 1 17 51 0 4 9 9 0 1	4

 

Задача D. Ковзанярська траса.

   Нарешті зима прийшла і до Хмеляндії. Адміністрація вирішила побудувати ковзанярську трасу в центральному парку, який представляє собою прямокутник розміром N на N метрів, розділений на квадрати однакового розміру площею один м2. Іншими словами парку відповідає прямокутна таблиця з N рядками і M стовпцями. Рядки нумеруються зверху вниз, починаючи з одиниці, стовпці нумеруються зліва направо, починаючи з одиниці. Отже, кожному квадрату можна поставити у відповідність пару числа (X, Y), де X - це номер рядка, а Y - номер стовпця, на перетині яких він знаходиться.
   Всі квадрати парку діляться на два типи: ті, що містять дерево або ті, що не містять дерево (порожній квадрат). Будемо вважати, що якщо квадрат містить дерево, то воно займає всю його площу.
Довжиною траси будемо вважати кількість квадратів, через які проходить траса. Ковзанярська траса повинна мати квадратну форму, причому її довжина повинна бути не менше L метрів, а ширина - рівно один метр. Межі траси повинні бути паралельні межі парку і проходити по лініях, які розділяють його на квадрати. Траса не може проходити через квадрати, які містять дерева.

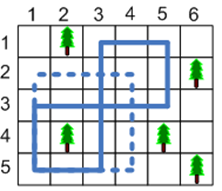
   На малюнку вище наведений приклад трьох можливих розміщень траси.

   Вам дано числа N, M, L, опис всіх квадратів парку, тобто для кожного з квадратів відомо, порожній він чи ні. Вам потрібно визначити кількість різних способів побудови ковзанярської траси. Способи вважаються різними, якщо їм відповідають різні множини квадратів.

   Вхідні дані:
   Перший рядок містить три цілих числа, розділені одиночними пробілами N, M (2 ≤ N, M ≤ 1000) і L (2 ≤ L ≤ 10⁹) відповідно. Наступні N рядків містять рядкові величини, що складаються з M символів, що описують парк, j-й символ в i-му за рахунком рядку описує тип квадрата. Символ '.' (ASCII 46) - квадрат з координатами (i, j) є порожнім, символ '#' (ASCII 35) - квадрат з координатами (i, j) містить дерево.

   Вихідні дані:
   Виведіть одне ціле число - кількість різних способів побудови ковзанярської траси.

   Приклади

Вхідні дані	Вихідні дані
5 6 8 .#.... .....# ...... .#..#. .....#	3
6 5 9 #.... ...#. ..... ..... ..#.. .....	3

 

Задача E. Святкові прикраси.

   Нещодавно на заводі святкових прикрас зібрали першу модель прикраси з різнокольорових лампочок, що світяться. Прототип прикраси збирався в такий спосіб: спочатку взяли дві лампочки і проводом з'єднали між собою, потім N-2 рази брали лампочку і з'єднували дротом з однією з раніше доданих до гірлянди лампочок. У підсумку вийшла прикраса з N різнокольорових лампочок. На заводі є лампочки К різних кольорів.
   Коли прототип був готовий, його передали Відділу надання краси. У цьому відділі було прийнято рішення вважати красою прикраси кількість пар лампочок одного кольору, з'єднаних дротом.
   Співробітники Відділу надання краси М раз перефарбовують деякі з лампочок в один з К кольорів з якихось, тільки їм відомим, міркувань. Все, що їм потрібно для випуску ідеальної прикраси - це швидко визначати красу виробу, після перефарбовування чергової лампочки.

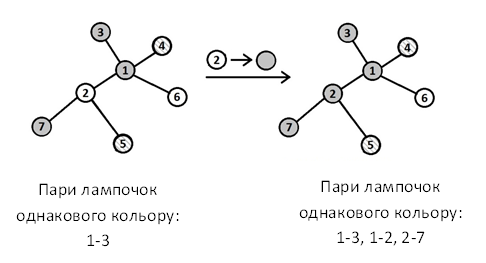
   Співробітники відділу надання краси просять Вас, кращого програміста написати програму, яка за заданим прототипом прикраси і послідовності перефарбування лампочок буде визначати красу прикраси.

   Вхідні дані:
   Перший рядок містить три цілих числа N, М, K (2 ≤ N ≤ 300 000, 1 ≤ М ≤ 300 000, 1 ≤ K ≤ 10⁹) - кількість лампочок в прототипі виробу, кількість перефарбовувань і кількість різних кольорів лампочок, наявних на заводі.
   Другий рядок містить N цілих позитивних чисел Ai (1 ≤ Ai ≤ К) - кольори лампочок в порядку додавання до виробу.
   Третій рядок містить N-2 цілих додатних чисел Рj (1 ≤ Pj ≤ j + 1) - номер лампочки, до якої була приєднана (j + 2)-а лампочка.
   Наступні М рядків містять по два цілих числа X і Y (1 ≤ Х ≤ N, 1 ≤ Y ≤ К) - номер лампочуи, що перефарбовується і колір, в який її перефарбовують, відповідно.
   Числа в рядках розділені одиночними пробілами.

   Вихідні дані:
   Виведіть М рядків. i-й рядок має містити єдине ціле число - кількість пар лампочок одного кольору, з'єднаних дротом, після виконання i перефарбовувань.

   Приклади

Вхідні дані	Вихідні дані
3 3 3 1 2 3 2 2 1 3 1 2 2	1 2 0
7 1 4 2 1 2 4 4 1 2 1 1 2 1 2 2 2	3

   Пояснення:

   Перший приклад:
   Всі лампочки з'єднані в ланцюжок (перша-друга-третя) і мають різні кольори. Далі їх перефарбовують в однаковий колір. Спочатку пара лампочок 1 2 стає однокольоровою (друга лампочка перефарбована в колір 1), а потім і 2 3 (третя лампочка перефарбована в колір 1). Після перефарбовування другої лампочки в колір 2 однокольорових пар лампочок, з'єднаних дротом, не залишається.

   Другий приклад:
   Приклад відповідає малюнку з умови.